Boolean Algebra Fundamentals for Digital Circuit Design: Complete Guide with Examples

Master Boolean algebra fundamentals for digital circuit design with practical examples and interactive simulations. Learn how to simplify logic expressions and design efficient digital circuits.

What is Boolean Algebra?

Boolean algebra, named after mathematician George Boole, is the foundation of digital electronics and computer science. It deals with binary values (1 and 0, or TRUE and FALSE) and forms the mathematical basis for all digital circuit operations.

Basic Boolean Operations

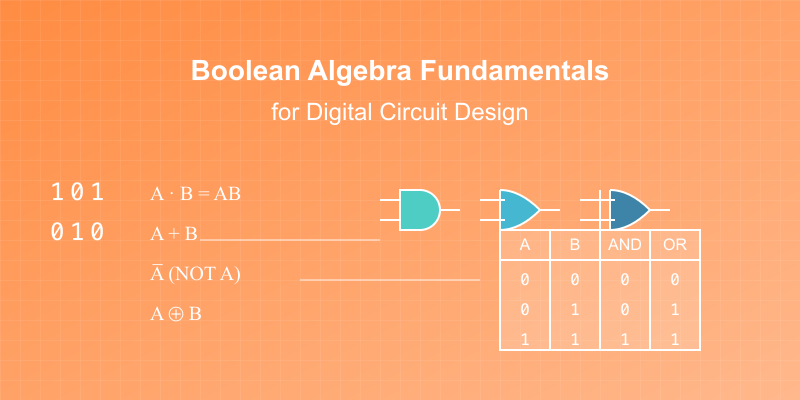
1. AND Operation (·)

A · B = 1 only when both A AND B are 1
Truth Table:
A B | Output
0 0 | 0
0 1 | 0
1 0 | 0
1 1 | 1

2. OR Operation (+)

A + B = 1 when either A OR B (or both) are 1
Truth Table:
A B | Output
0 0 | 0
0 1 | 1
1 0 | 1
1 1 | 1

3. NOT Operation (')

A' = opposite of A
Truth Table:
A | Output
0 | 1
1 | 0

AND, NOT & OR Gate Interactive Example - Try it now

Essential Boolean Laws and Theorems

These laws form the foundation of digital logic design and are used extensively in simplifying complex boolean expressions, designing circuits, and optimizing computer operations. They're particularly useful when minimizing logic circuits to use fewer gates or when simplifying complex logical conditions in programming.

• Identity Laws
  • A + 0 = A: When you OR ("+") anything with 0, it remains unchanged. Like if you have a light switch that's ON (1) and combine it with OFF (0), the result is still ON.
  • A · 1 = A: When you AND ("·") anything with 1, it remains unchanged. Similar to multiplying any number by 1 in regular math.
• Complement Laws
  • A + A' = 1: When you OR something with its opposite (complement), you always get 1 (TRUE). Think of it as "either it's raining OR it's not raining" - this is always true.
  • A · A' = 0: When you AND something with its opposite, you always get 0 (FALSE). Like "it's raining AND it's not raining" - this can never be true.
• Commutative Laws
  • A + B = B + A: The order doesn't matter in OR operations. "Either Bob or Alice will attend" means the same as "Either Alice or Bob will attend."
  • A · B = B · A: The order doesn't matter in AND operations. "It's sunny and warm" means the same as "It's warm and sunny."
• Associative Laws
  • (A + B) + C = A + (B + C): When using OR, you can group terms differently and get the same result. Like saying "(I'll bring chips or drinks) or dessert" is the same as "I'll bring chips or (drinks or dessert)."
  • (A · B) · C = A · (B · C): Same for AND operations. "(The car is red and fast) and new" means the same as "The car is red and (fast and new)."
• Distributive Laws
  • A · (B + C) = (A · B) + (A · C): Similar to regular algebra. "I want a car that is (red or blue)" means the same as "(I want a red car) or (I want a blue car)."
  • A + (B · C) = (A + B) · (A + C): The OR version of distribution. "Either it's sunny OR (it's cold AND windy)" means the same as "(it's sunny OR cold) AND (it's sunny OR windy)."

Boolean Expression Simplification

Let's walk through a practical example:

Let's start with: F = A·B + A·B'C + A·BC

1. Factor out common terms (Step 1)
   • Looking at each term, we can see 'A' appears in all of them
   • So we can factor out A: F = A·(B + B'C + BC)
   • This is like factoring in regular algebra, where we pull out common terms
   • We use the distributive law in reverse: A·X + A·Y = A·(X + Y)
2. Simplify within parentheses (Step 2)
   • Inside the parentheses, we have: B + B'C + BC
   • The term BC is absorbed by B (absorption law states X + XY = X)
   • Why? Because if B is true:
     • If B is 1, then B + BC = 1 + C = 1 (which is just B)
     • If B is 0, then B + BC = 0 + 0 = 0
   • So B + BC simplifies to just B
   • We're left with B + B'C
3. Final expression (Step 3)
   • Our final simplified expression is: F = A·(B + B'C)
   • This is simpler than our original expression
   • It requires fewer logic gates to implement
   • It's easier to understand and work with

Let's verify this is correct by testing some cases:

• When A = 0: The whole expression is 0 (matches original)
• When A = 1 and B = 1: Result is 1 (matches original)
• When A = 1, B = 0: Result depends on C (matches original)

This simplification process is crucial in:

• Digital circuit design (fewer gates needed)
• Computer programming (more efficient conditions)
• Logic optimization (clearer logical statements)

De Morgan's Theorems

1. (A + B)' = A' · B'
   • This states that the complement of a sum (OR) equals the product (AND) of the complements
   • Real-world example: "Not (sunny OR warm)" means "Not sunny AND not warm"
   • Circuit example: Instead of using an OR gate followed by a NOT, you can use two NOT gates and an AND gate
2. (A · B)' = A' + B'
   • The complement of a product (AND) equals the sum (OR) of the complements
   • Real-world example: "Not (tall AND blonde)" means "Not tall OR not blonde"
   • Very useful in converting between NAND and NOR logic

Karnaugh Maps (K-Maps):

1. 2-Variable K-Map:

   B  B'
A  |1 |0 |
A' |0 |1 |

• Used for expressions with 2 variables
• Adjacent cells differing by one variable can be grouped
• Each group represents a term in the simplified expression

2. 3-Variable K-Map:

B'C' B'C  BC   BC'
A'   |0   |1   |1   |0  |
A    |1   |1   |0   |0  |

• Handles expressions with 3 variables
• Groups can wrap around edges
• Larger groups mean simpler expressions

Practical Applications

1. Simple Alarm System:

• Inputs: Door sensor (D), Motion sensor (M), Armed status (A)
• Output: Alarm (Y)
• Boolean expression: Y = A·(D + M)
• Means: Alarm triggers if system is armed AND (door opens OR motion detected)

2. Voting System:

• Inputs: Voter 1 (V1), Voter 2 (V2), Voter 3 (V3)
• Output: Decision (D)
• Majority logic: D = V1·V2 + V2·V3 + V1·V3
• Can be simplified using K-map

Common Digital Design Patterns:

1. Multiplexer (MUX):

• Selects between multiple inputs based on selection lines
• Boolean expression: Y = S'·A + S·B
• Used in data routing and arithmetic circuits

2. Full Adder:

• Three inputs: A, B, Carry-in (Cin)
• Two outputs: Sum (S), Carry-out (Cout)
• Sum: S = A ⊕ B ⊕ Cin (XOR)
• Carry: Cout = (A·B) + (Cin·(A ⊕ B))
• Basic building block for arithmetic operations

These concepts are fundamental to:

• Digital circuit design
• Computer architecture
• Logic optimization
• Electronic system design

Tips for Circuit Optimization

1. Always simplify before implementation
2. Use K-maps for expressions with up to 4 variables
3. Look for common terms
4. Apply De Morgan's theorems for complemented functions

Try It in Scratchboard

Practice these concepts in our interactive simulator:

• Design and test logic circuits
• Verify Boolean expressions
• Compare simplified vs. unsimplified circuits
• Share your solutions with others

Common Pitfalls to Avoid

1. Forgetting precedence rules
2. Incorrect application of De Morgan's theorems
3. Missing minimal solutions in K-maps
4. Overlooking don't-care conditions

Advanced Topics

• Binary Arithmetic
• Sequential Logic
• State Machines
• Timing Diagrams

Ready to master Boolean algebra? Sign up for Scratchboard and access our complete suite of interactive digital design tools.